Belajar tentang sifat dan rumus balok merupakan salah satu hal yang dipelajari saat Anda belajar matematika. Apabila diperhatikan, bentuk balok sendiri sebenarnya sangat familiar dalam kehidupan sehari-hari.
Anda dapat menemukan benda berbentuk balok seperti lemari, televisi, batu bata, dan lain sebagainya. Hal tersebut menunjukkan bahwa bangun tersebut sering digunakan dan Anda perlu untuk mengenalnya lebih jauh.
Berbagai informasi seperti unsur, sifat, sampai dengan rumus-rumus dari balok sangat penting untuk Anda ketahui. Nah, berikut adalah berbagai penjelasan tentang hal-hal yang perlu Anda ketahui mengenai bangun balok.
Apa Pengertian Balok?
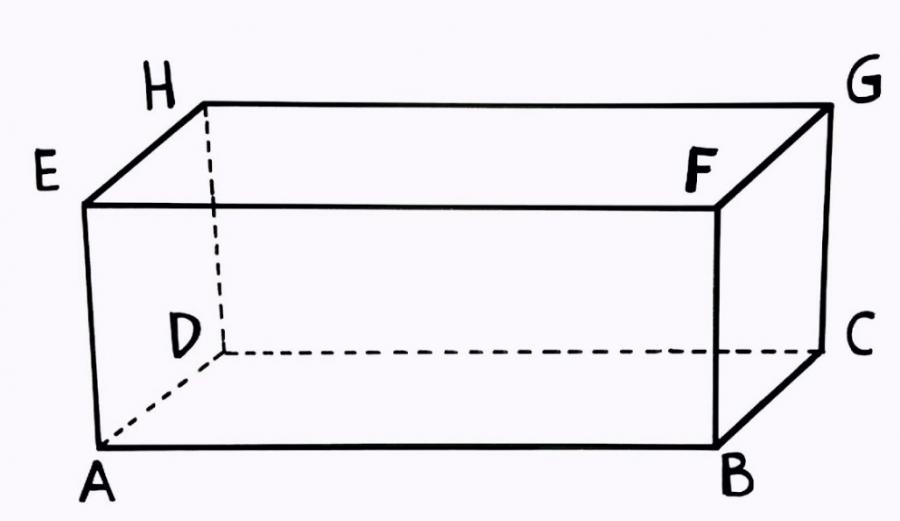
Hal pertama yang perlu diketahui tentang bangun ini adalah pengertiannya. Pengertian dari balok adalah suatu bangun ruang tiga dimensi yang tersusun atas tiga pasang persegi panjang yang mempunyai ukuran berbeda-beda.
Bangun ini biasanya juga dapat dimasukkan ke dalam kategori bentuk prisma. Sementara untuk prisma sendiri, mempunyai arti sebagai bangun ruang dengan bentuk atap dan alas yang ukurannya kongruen atau sama.
Secara umum, bangun ini disusun atas elemen panjang (rusuk terpanjangnya), lebar (rusuk terpendek sisinya), dan juga tinggi (rusuk yang tegak lurus dengan panjang dan lebarnya). Ketiga elemen tersebut akan berperan penting dalam sifat hingga rumus perhitungannya nanti.
Sementara untuk ciri khusus dari bentuk ini adalah sebagai berikut:
- Mempunyai 6 bagian sisi
- Rusuk balok ada 12
- 8 titik sudut
- 12 diagonal bidang
- 4 diagonal ruang
- Dan 6 bidang diagonal
Semua ciri tersebut perlu dipahami secara mendalam supaya Anda dapat membedakannya dengan bangun lainnya. Ciri-ciri tersebut juga bisa menjadi suatu karakter khas dari suatu bidang yang memenuhi kriteria untuk disebut sebagai balok.
Mengenal Sifat-Sifat Balok
Balok mempunyai beberapa sifat khusus yang membuatnya berbeda dengan jenis bangun ruang lainnya. Sifat tersebut wajib untuk Anda ketahui saat mempelajari tentang bangun ruang ini. Selain untuk lebih mengenalnya, sifat tersebut nanti juga berguna dalam perhitungan.
Berikut ini adalah beberapa sifatnya:
- Sisi balok mempunyai bentuk persegi panjang
- Rusuk yang posisinya sejajar mempunyai ukuran panjang yang sama
- Semua diagonal bidang sisinya yang saling berhadapan mempunyai ukuran panjang sama
- Semua bidang diagonal dari bangun ini mempunyai bentuk persegi panjang
- Semua diagonal ruang bangun ini mempunyai ukuran sama panjang
Perhatikan dan pahami betul sifat-sifat yang disebutkan di atas. Dengan memahaminya dengan benar, nantinya dapat memudahkan Anda dalam mengerjakan soal balok baik untuk menghitung keliling, luas permukaan, hingga perhitungan volume-nya.
Mengenal Rumus Balok
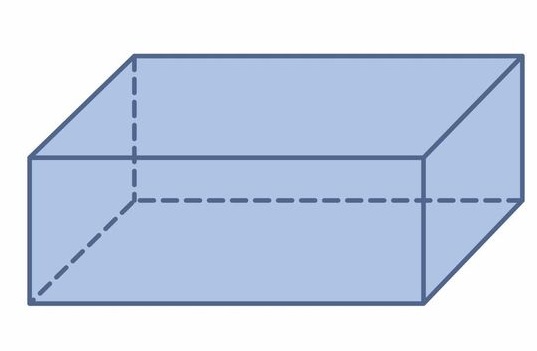
Setelah mengetahui tentang pengertian, sifat, dan juga ciri-cirinya, selanjutnya akan diberikan juga tentang rumus balok. Rumus tersebut meliputi perhitungan volume, keliling, diagonal balok, dan juga luas permukaannya.
1. Volume
Volume merupakan isi atau daya tampung dari suatu bangun ruang. Rumus volume dari bangun balok secara umum dapat dicari dengan mengalikan luas dari alasnya dengan tinggi.
Oleh karena alas dari bangun ini mempunyai bentuk persegi panjang, maka dalam mencari luas alasnya akan menggunakan rumus luas persegi panjang, yakni panjang dikali lebar. Jadi, untuk mencari volume dari bangunnya dapat digunakan rumus berikut.
Rumus Volume Balok:
V = p x l x t
2. Keliling
Keliling merupakan hasil penjumlahan dari semua panjang rusuk dari balok. Oleh karena itu, pencarian dari panjang keliling tersebut sama saja dengan menjumlahkan semua panjang dari rusuknya.
Dengan kata lain, rumus kelilingnya bisa dituliskan seperti berikut:
Keliling Balok = 4p + 4l + 4t atau bisa disederhanakan menjadi 4 (p + l + t)
3. Panjang Diagonal Balok
Berikutnya akan diberikan juga rumus untuk mengetahui rumus diagonal pada balok seperti mencari diagonal sisi depan, sisi samping, alas, dan diagonal ruang. Rumus seperti ini biasanya juga diberikan pada saat memasuki jenjang sekolah menengah hingga atas.
Bagi yang belum tahu, diagonal ruang balok merupakan ruas garis penghubung dua buah titik sudut yang saling berhadapan di dalam balok. Lebih lanjut, berikut adalah rumus perhitungan diagonal ruang tersebut:
Rumus Diagonal Ruang, d = √(p² + l² + t²)
Sedangkan untuk menentukan dari panjang diagonal sisinya, dapat menggunakan rumus berikut:
- panjang diagonal sisi depan = √(p² + t²)
- panjang diagonal sisi samping = √l² + t²)
- panjang diagonal sisi alas = √(p² + l²)
4. Luas Permukaan
Rumus terakhir yang akan diberikan adalah untuk mencari luas dari permukaan bangunnya. Seperti diketahui, balok tersusun atas 6 bangun persegi panjang sepasang dan kongruen.
Persegi panjang kongruen tersebut antara lain adalah bagian alas dan tutup, bidang sisi kanan dan kiri, serta bagian sisi belakang dan depan. Berdasarkan hal tersebut, dapat diketahui cara untuk menghitung luas permukaannya sebagai berikut.
Luas Permukaan = Luas bagian alas dan tutup + luas sisi kanan dan kiri + luas sisi belakang dan depan
Atau bisa dituliskan perhitungan tersebut menjadi rumus berikut:
Rumus Luas Permukaan = 2 (pl + pt + lt)
Contoh Soal Menghitung Balok

Untuk memperjelas pemahaman tentang rumusnya, akan diberikan juga beberapa contoh soal. Berikut adalah contoh soal perhitungan baloknya:
1. Contoh 1
Terdapat kardus dengan bentuk balok dengan ukuran panjang 30 cm, lebar 20 cm, dan tingginya 10 cm. Hitunglah luas permukaan dari kardusnya!
Jawaban:
Dalam menghitung permasalahan di atas, dapat digunakan rumus umum menghitung luas permukaan, yakni 2(pl + pt + lt). Pada soal dijelaskan kardus tersebut mempunyai panjang 30 cm, lebarnya 20 cm, serta tingginya 10 cm. Dengan menggunakan rumusnya, perhitungannya menjadi seperti berikut.
Luas Permukaan kardus = 2 (pl + pt + lt)
= 2 (30.20 + 30.10 + 20.10)
= 2 (600 + 300 + 200)
= 2 (1100)
= 2200 cm2
Dari perhitungan tersebut didapatkan bahwa luas permukaan kardusnya adalah 2200 cm2.
2. Contoh Soal 2
Diketahui sebuah balok mempunyai ukuran panjang 6 cm, lebar 4 cm, dan tingginya 2 cm. Berdasarkan informasi tersebut, hitunglah volume dari baloknya!
Jawaban:
Untuk mencari volume dapat menggunakan rumus panjang kali lebar kali tinggi. Dari soal di atas, diketahui bahwa panjang dari baloknya adalah 6 cm, lebarnya 4 cm, dan tingginya 2 cm. Berdasarkan hal tersebut, dapat dihitung volumenya seperti berikut.
Volume = Panjang x Lebar x Tinggi
= 6 cm x 4 cm x 2 cm
= 48 cm3
Jadi, dapat diketahui bahwa volume dari balok tersebut adalah 48 cm3.
Dari kedua contoh soal di atas diharapkan Anda dapat lebih memahami bagaimana menerapkan rumus volume sampai dan mencari luas permukaan baloknya.
Berdasarkan semua penjelasan di atas, Anda dapat mengetahui pengertian, sifat, ciri, dan rumus balok dengan lebih jelas lagi. Ditambah lagi adanya contoh soal beserta jawabannya membuat Anda lebih mudah dalam memahami penerapan rumusnya.
Namun untuk benar-benar paham dan mengerti tentang penerapan rumusnya tentu tidak boleh hanya berdasar dua contoh di atas. Semakin banyak contoh soal yang dikerjakan, maka itu akan membuat Anda semakin mudah untuk memahami bab bangun ruang ini.