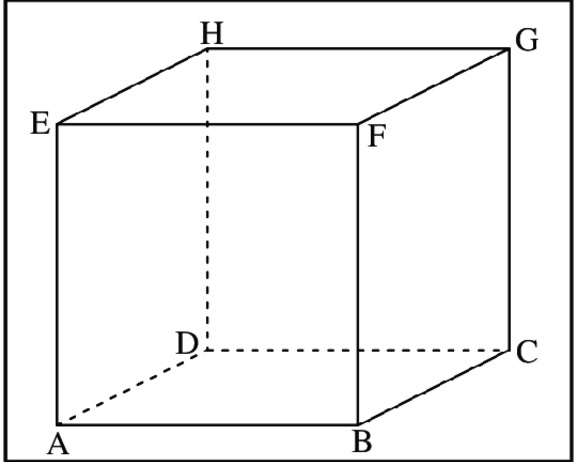
Mempelajari tentang rumus kubus dan ciri-cirinya merupakan hal yang pasti ditemui saat belajar matematika. Kubus sendiri merupakan bangun ruang tiga dimensi dengan enam sisi persegi berukuran sama.
Bangun ini mempunyai delapan titi sudut sama dan 12 rusuk dengan panjang sama. Setiap sudut antara dua rusuk yang bertemu mempunyai besar sudut 90 derajat atau biasa disebut dengan siku-siku.
Memahami tentang rumus dan ciri dari bangun ini akan membuat Anda lebih mudah untuk mengerjakan perhitungannya. Berikut adalah berbagai macam ciri, rumus, dan juga contoh soalnya.
Ciri-Ciri Kubus

Seperti halnya bangun ruang lainnya, kubus pastinya mempunyai ciri khusus yang membedakannya dengan bangun lainnya. Berikut adalah berbagai macam ciri yang perlu diketahui tentang bangun ruang tersebut.
1. Rusuk
Berikutnya, bangun ini mempunyai rusuk sebanyak 12 sama panjang. Panjang sama tersebut dapat terjadi karena memang bangun ini tersusun dari persegi yang mempunyai sisi sama panjang.
2. Simetri
Jumlah bidang simetri dari bangun ini adalah 6 yang terbagi sama besar. Maksudnya adalah meskipun diputar ataupun diubah posisinya namun bentuknya tetaplah sama seperti awal.
3. Sudut
Ciri berikutnya adalah bangun ruang ini mempunyai 8 sudut sama besar. Perlu diketahui kubus tersusun atas 6 persegi dan 4 sudutnya sama besar. Keenam persegi tersebut membentuk sudut sama besarnya.
4. Diagonal
Ciri berikutnya adalah terdapat dua jenis diagonal, yakni diagonal sisi dan ruang. Jumlah diagonal ruangnya ada 4 yang berpotongan di bagian tengah ruang kubusnya. Sementara diagonal sisinya ada 12 garis yang berpotongan di sisi kubusnya.
5. Sisi
Sementara ciri berikutnya adalah kubus memiliki 6 sisi datar sama besar. Sisi tersebut mempunyai bentuk persegi dengan panjang sisinya sama. Sisi tersebut juga membentuk segiempat datar, di mana semua sudutnya mempunyai besar 90 derajat.
Berbagai ciri di atas merupakan karakter khas dari bangun ruang ini. Dengan memahami tentang ciri-ciri tersebut, Anda bisa mengenali seperti apa karakter dan bentuk dari bangun tersebut secara lebih mudah.
Apa Saja Rumus Kubus?

Selain mencari tahu tentang apa saja ciri-cirinya, Anda tentu juga harus memahami juga tentang rumus kubus. Anda perlu mengetahui tentang rumus volume, luas, luas permukaannya, dan juga kelilingnya.
Rumus tersebut tentu sangat penting untuk diketahui agar Anda dapat lebih mudah untuk mengerjakan berbagai soal perhitungannya. Nah, berikut ini adalah berbagai macam rumus tentang kubus yang perlu untuk diketahui.
1. Luas Permukaan
Luas permukaan kubus merupakan jumlah total luas semua sisinya. Seperti dijelaskan di awal, kubus mempunyai enam sisi dengan panjang sama besar. Berdasarkan hal tersebut maka dapat diketahui bahwa untuk menghitung luas permukaannya maka tinggal kalikan saja luas persegi dengan enam.
Rumusnya dapat ditulis seperti berikut.
Luas Permukaan = 6(sisi x sisi) = 6s2, s adalah sisi perseginya.
2. Rumus Keliling
Untuk menghitung keliling dari kubus Anda tinggal menjumlahkan saja semua panjang rusuknya. Seperti diketahui sebelumnya, bangun ini mempunyai enam sisi maka untuk mendapatkan berapa kelilingnya tinggal kalikan saja sisinya dengan enam, dengan s adalah panjang sisinya
Rumus Keliling = 6s, dengan s adalah sisi kubusnya.
3. Luas Bagian Sisi
Kubus mempunyai sisi sama besar dengan bentuk persegi. Oleh karena itu, untuk menghitung luas dari salah satu sisinya cukup dengan memakai rumus perhitungan luas persegi. Jadi, rumusnya adalah panjang sisi dikalikan sisi atau s x s, dengan s adalah panjang sisi.
Luas Bagian Sisi Kubus = s2
4. Rumus Kubus Volume
Terakhir ada rumus untuk menghitung volume dari kubus. Untuk menghitung volume kubusnya digunakan rumus sisi x sisi x sisi atau bisa disebut dengan s3, dengan s adalah panjang sisi.
Volume Kubus = s3
Contoh Soal Kubus
Supaya lebih paham dan jelas tentang bangun kubus, diperlukan contoh soal penerapannya. Dengan memahami pengerjaan soal tersebut, pastinya Anda dapat lebih jelas dengan penggunaan dari rumus-rumusnya.
Berikut adalah contoh soalnya:
1. Contoh 1
Diketahui sebuah kubus mempunyai sisi dengan panjang 5 cm. Berikutnya, hitunglah luas permukaan dan volume dari kubus tersebut!
Jawab:
Diketahui: panjang kubusnya adalah 5 cm
Ditanyakan: berapa volume dan luas permukaannya?
Dijawab:
Untuk menghitung volume kubusnya menggunakan rumus:
Volume = s3 = 5 x 5 x 5 = 125 cm3
Sementara untuk luas permukaannya menggunakan rumus:
Luas permukaan = 6 x s2 = 6 x (5 x 5) = 150 cm2
Dari perhitungan di atas dapat diketahui bahwa volume kubusnya adalah 125 cm3 dan luas permukaannya adalah 150 cm3.
2. Contoh 2
Terdapat sebuah kubus dengan panjang kelilingnya adalah 24 cm. Berdasarkan hal tersebut, carilah panjang sisi, luas salah satu sisinya, dan juga volume dari kubusnya!
Jawab:
Diketahui: Sebuah kubus dengan panjang kelilingnya 24 cm
Ditanyakan: Berapa panjang sisinya, volume, dan luas salah satu sisinya
Dijawab:
Telah diketahui bahwa panjang kelilingnya adalah 24 cm. Berdasarkan keliling tersebut dapat dicari panjang sisi seperti berikut:
Keliling = 6s = 24
Jadi, panjang sisinya adalah s = 24 / 6 = 4 cm
Setelah diketahui panjang sisinya adalah 4 cm, berikutnya dapat dihitung volum serta luas salah satu bagian sisinya sebagai berikut:
Volume = s3 = 4 x 4 x 4 = 64 cm3
Luas salah satu sisinya = s2 = 4 x 4 = 16 cm2
Selesai.
3. Contoh 3
Terdapat sebuah kardus berbentuk kubus dengan luas permukaannya sebesar 294 cm2. Dari informasi tersebut, hitunglah panjang sisinya, luas permukaan dan volume kubus!
Jawab:
Diketahui: ada sebuah kardus kubus dengan luas permukaan sebesar 294 cm2.
Ditanyakan: Hitunglah keliling, volume, serta panjang sisinya
Dijawab:
Pada soal telah diketahui luas permukaanya sebesar 294 cm2. Berdasarkan informasi tersebut dapat dicari panjang sisinya dengan cara berikut.
Luas permukaan = 6 x s2 = 294 cm2, dari persamaan tersebut dapat dicari sisinya dengan rumus:
S = √(294/6) = √49 = 7 cm
Selanjutnya tinggal hitung volume dan kelilingnya:
Volume = s3 = 73 = 343 cm3
Keliling = 6s = 6 x 7 = 42 cm
Jadi, dari perhitungan di atas diperoleh bahwa panjang sisinya adalah 7 cm, kelilingnya 42 cm, dan volume kubusnya adalah 343 cm3.
Kurang lebih seperti itulah contoh perhitungan dari rumusnya. Dengan melihat contoh tersebut tentu diharapkan Anda dapat lebih mudah untuk memahami bagaimana penerapan dari rumusnya.
Berdasarkan penjelasan di atas, kini Anda dapat mengetahui ciri-ciri dan juga rumus kubus. Rumus yang perlu diketahui terkait kubus antara lain adalah volume, luas permukaan, keliling, dan juga luas salah satu bagian sisinya.
Secara keseluruhan, berbagai rumus tersebut dapat diaplikasikan secara sederhana. Untuk memahami bagaimana penggunaannya, Anda bisa melihatnya pada contoh soal yang sudah diberikan sebelumnya.